97. De Morgan, sống vào thế kỉ 19, từng nêu câu đố sau đây về tuổi của ông:
Tôi x tuổi vào năm x2. Hỏi tôi sinh năm bao nhiêu?
Câu đố là một câu hỏi nêu ra có vẻ bí hiểm.
Bình phương các tuổi có thể được lập như sau. Bắt đầu với 40, ta có
402 = 1600
412 = 1681
422 = 1764
432 = 1849
442 = 1936
Vì De Morgan sống vào thế kỉ 19, tức là trong giai đoạn 1801-1900, nên ông 43 tuổi vào năm 1849, và do đó, ông sinh vào năm 1806.
98. Các hệ phương trình vô định được giải như thế nào?
Khi cho hai phương trình vô định theo ba biến, thì một biến bất kì, ví dụ z, được loại trừ và ta thu được một phương trình vô định hai biến.
Phương trình đó được giải như thường lệ.
Xét bài toán sau đây:
Chi phí cho một bữa tiệc 44 người là 451 rupee. Nếu mỗi người đàn ông chi 15 rupee, mỗi phụ nữ chi 12 rupee và mỗi trẻ em chi 5 rupee, thì có bao nhiêu người thuộc mỗi nhóm?
Gọi x, y, z lần lượt là số lượng đàn ông, phụ nữ và trẻ em, thì ta có
x + y + z = 44 (1)
15x + 12y + 5z = 451 (2)
Nhân phương trình thứ nhất với 5 rồi trừ khỏi phương trình thứ hai để loại trừ z, ta được
10x + 7y = 231 (3)
Đây là một phương trình hai biến và có thể giải cho các giá trị nguyên dương như thông thường.
Chia phương trình cho hệ số nhỏ là 7, ta được
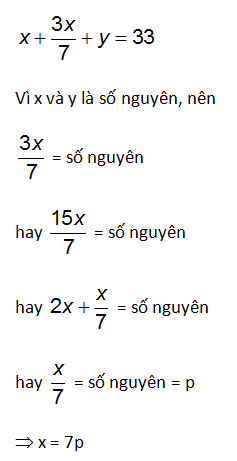
Thay giá trị này của x vào (3), ta được y = 33 – 10p.
Thay x và y vào (1) ta được z = 3p + 11.
Bây giờ, p chỉ có thể nhận các giá trị 1, 2 và 3, bởi vì các giá trị lớn hơn của p khiến y bị âm.
Như vậy, nghiệm đầy đủ được cho bởi
p = 1, x = 7, y = 23, z = 14;
p = 2, x = 14, y = 13, z = 17;
p = 3, x = 21, y = 3, z = 20.
99. Phương trình sau đây được giải như thế nào theo nghiệm dương:
2xy – 4x2 + 12x – 5y = 11?
Phương trình đã cho có thể được viết là
2xy – 5y = 4x2 – 12x + 11
hay (2x – 5)y = 4x2 – 12x + 11
Biểu diễn y theo x, ta được

Vì ± 1, ± 2, ± 3 và ± 6 là những ước số duy nhất của 6, nên
2x – 5 = ± 1, ± 2, ± 3 và ± 6.
Trong số này 2x – 5 = ± 2 và ± 6 không mang lại giá trị nguyên của x, và buộc phải loại bỏ.
2x – 5 = ± 1 và 2x – 5 = ± 3 cho x = 3, 2, 4 và 1.
Những giá trị này cho ta:
x = 3, y = 11; x = 2, y = - 3;
x = 4, y = 9; x = 1, y = - 1.
Trong số này, các nghiệm có thể nhận là
x = 3, y = 11; x = 4, y = 9.
100. Phương trình vô định tổng quát bậc hai là gì?
Phương trình bậc hai: Ny2 + 1 = x2,
trong đó N là một số nguyên dương nhưng không phải số chính phương, được gọi là phương trình vô định tổng quát bậc hai.
Nó luôn có thể được giải theo nghiệm nguyên dương, số lượng nghiệm là không hạn chế.
Phương pháp giải nghiệm hơi khó và không thích hợp để nêu ra ở đây.
101. Phương trình 61y2 + 1 = x2 có gì nổi bật?
Đây là một trường hợp đặc biệt của phương trình tổng quát vừa nói ở trên, trong đó N nhận giá trị 61.
Bhaskaracharya, nhà toán học vĩ đại người Hindu, nổi tiếng với việc thu được nghiệm nguyên tổng quát của phương trình này bởi cái gọi là “phương pháp tuần hoàn”.
Để minh họa cho phương pháp đó, trong quyển sách của ông, “Bija ganita”, được viết vào năm 1150, ông đã nêu ví dụ 61y2 + 1 = x2.
Cái nổi bật là 500 năm sau đó, bài toán này lại được nhà toán học lỗi lạc người Pháp Fermat nêu ra cho người bạn của ông, Frenicle, vào năm 1657.
Nhưng rồi nó được Euler giải vào năm 1732.
Bhaskaracharya nêu ra nghiệm sau đây:
x = 1, 776, 319, 049,
y = 22, 615,390
Toán học – Những điều kì thú và những mốc son lịch sử
A.L. Audichya
Trần Nghiêm dịch
Phần tiếp theo >>