Chương 13
OMEGA
Điều hợp lí là chương cuối của quyển sách này nên dành để nói về hằng số mô tả số phận tối hậu của vũ trụ. Hợp lí không chỉ bởi vì omega là kí tự cuối trong bảng chữ cái Hi Lạp, mà nó còn là hằng số có giá trị, một khi đã biết, sẽ cho chúng ta biết chúng ta đang sống trong một vũ trụ đi đến giãn nở mãi mãi hay sẽ co lại – và có khả năng tái sinh. Tất nhiên, là một nhà toán học, tôi là một fan cuồng hâm mộ đối xứng, cho nên tôi có chút hài lòng khi để quyển sách này bắt đầu với một chương về lực hấp dẫn, và kết thúc cũng với một chương về lực hấp dẫn.
Đa số mọi người ngày nay – và có lẽ trong bất kì thời đại nào không quá tồi tệ - lấy hiện tại là trung tâm, họ tin rằng thời đại hiện tại cho dù không phải là thời đại tốt nhất, nhưng nó vẫn tiến bộ vượt bậc so với những thời đại trước đó. Tôi chắc chắn là một người như thế. Tôi thích có Internet, truyền hình cáp, thức ăn Trung Hoa, nha khoa không đau, và đi máy bay. Tôi cũng cảm thấy kinh ngạc trước những gì chúng ta biết, và chúng ta đã biết bao nhiêu về vũ trụ trong khoảng thời gian ngắn kể từ khi tôi chào đời. Kiến thức của chúng ta quá mênh mông, và các công cụ của chúng ta dùng để tìm kiếm và khai thác nó là quá mạnh, nên có thể khó mà tưởng tượng nổi làm thế nào người ta có thể làm được việc gì, hay làm đúng, mà không có chúng.
Thuyết tương đối rộng Einstein
Một trong những ấn tượng sơ bộ của thuyết tương đối rộng Einstein là đã có thời nó hết sức khó hiểu nên chỉ có chừng một tá người trên thế giới hiểu được nó. Thật vậy, khi có người hỏi Eddington rằng ông nghĩ sao trước phát biểu rằng chỉ có ba người hiểu được thuyết tương đối, người ta đồn rằng ông đã hỏi lại vậy ai là người thứ ba. George Ellery Hale, giám đốc Đài thiên văn Núi Wilson, đã đổ thêm dầu vào lửa khi ông nói, “Những cái phức tạp của thuyết tương đối rộng khiến tôi khó lĩnh hội nỗi.”
Nhưng Steven Weinberg, người giành giải Nobel Vật lí và là tác giả của quyển Ba phút đầu tiên, không tán thành như thế. Ông viết, “Không bao giờ có chuyện chỉ có một tá người hiểu được những bài báo của Einstein về thuyết tương đối rộng, nhưng nếu đúng như vậy, thì đó sẽ là một thất bại của Einstein, chứ không phải một điểm nhấn cho sự lỗi lạc của ông.” Thuyết tương đối rộng ngày nay được xem là một môn học chính trong ngành vật lí, mặc dù nó khó hiểu đối với các chuyên gia, nhưng đa số các nhà vật lí thuộc thời đại Einstein cũng đều là những nhà vật lí bậc thầy.
Tuy nhiên, các phương trình trường Einstein (EFE), trái tim toán học của thuyết tương đối rộng, thật sự là cái khó nuốt đối với dân không chuyên. Ví dụ, mô tả toán học ngắn gọn của chúng là: một hệ gồm mười sáu phương trình vi phân riêng kết hợp, phi tuyến, hyperbolic-elliptic. Vâng, đó là một và một nửa miếng bánh thơm – nhưng một miếng thì nước không trôi, còn nửa miếng kia thì đặt ở chỗ tay với không tới. Một số thuật ngữ thì dễ hiểu, một số khác đòi hỏi kiến thức giải tích – nhưng cho dù không biết giải tích thì người ta vẫn có khả năng cảm nhận EFE là cái gì.
Trước tiên, chúng là những phương trình, nhưng chúng không giống với những phương trình thông thường mà đa số mọi người quen thuộc, ví dụ như 2x + 5 = 7, nghiệm cho nó là một con số. Chúng là những phương trình mô tả tốc độ mà những thông số nhất định biến thiên tại ở những nơi khác nhau và tại những thời điểm khác nhau – đó là phần “phương trình vi phân riêng” – và nghiệm của chúng là những hàm số chứ không phải con số. Phần “hyperbolic-elliptic” đơn giản mô tả một loại phương trình vi phân riêng phần nhất định, kiểu giống như từ “bậc hai” dùng để mô tả một loại phương trình một biến nhất định.
“Kết hợp” có nghĩa đơn giản là các biến thường xuất hiện chung trong một phương trình. Ví dụ, trong hai phương trình dưới đây, các biến x và y không phải là kết hợp.
2x + 5 = 7
3y – 1 = 8
Tuy nhiên, trong các phương trình sau đây, các biến x và y là kết hợp
2x + y = 5
7x – 2y = 1
Những ai quen thuộc với đại số phổ thông đều biết rằng hai phương trình không kết hợp ở trên có thể được giải riêng, nhưng để giải hệ biến kết hợp đòi hỏi phải làm việc chung trên chúng, sử dụng một kĩ thuật đại số gọi là phép khử. Các phương trình kết hợp hầu như luôn luôn khó giải hơn các phương trình không kết hợp.
Cuối cùng, một phương trình tuyến tính là một phương trình ví dụ như 2x + 5 = 7 hay 2x + y = 5, trong đó toàn bộ các biến xuất hiện một mình; chúng không mang số mũ, cũng không có các hàm như logarithm áp dụng cho bất kì biến nào. Một phương trình phi tuyến ví dụ như x3 + 5x = 18 luôn luôn khó giải hơn một phương trình tuyến tính.
Sinh viên lớp cao thời Einstein chẳng gặp khó khăn gì trong việc giải mã khái niệm hệ phương trình vi phân riêng kết hợp, phi tuyến, hyperbolic-elliptic. Cái khiến nghiên cứu của Einstein quan trọng là tính khái quát của những hiện tượng mà nó mô tả, và chiều sâu kiến thức cần thiết để suy luận ra những phương trình đó.
Tuy nhiên, tôi không nghĩ bạn cần phải hiểu bất kì nội dung nào ở đây để thưởng thức cái đơn giản đẹp đẽ của của “ngôn ngữ” mà Einstein trình bày các kết quả của ông. EFE có thể viết đơn giản ở dạng
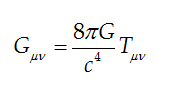
Kí hiệu G độc thân ở vế phải của phương trình và c là hằng số hấp dẫn và tốc độ ánh sáng. Những kí hiệu còn lại là tensor, đó là những cách viết cô đọng chứa rất nhiều thông tin; µ và n có giá trị từ 0 đến 3, trong đó 0 biểu diễn tọa độ thời gian ct (có một lí do kĩ thuật để nhân thời gian t với tốc độ ánh sáng) và 1 đến 3 biểu diễn các tọa độ không gian. Cả bốn tọa độ cùng mô tả một điểm duy nhất trong không-thời gian, một nơi được nêu rõ (bởi các tọa độ 1 đến 3) và một thời điểm được nêu rõ (bởi tọa độ 0). Thật ra, có tới 16 phương trình tương ứng với 16 cách khác nhau 00, 01,..., 23, 33 chọn một giá trị cho µ từ 1 đến 3 và một giá trị cho n từ 0 đến 3. Tuy nhiên, có một số cái thừa trong những phương trình này, và chúng có thể được giảm xuống còn sáu phương trình.
Những con số làm nên vũ trụ
James D. Stein
<< Phần trước | Phần tiếp theo >>















