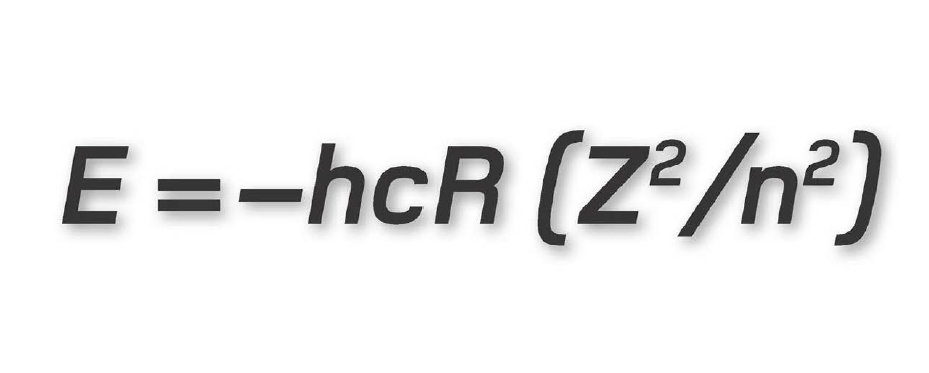Toán tử Hamiltonian
Một trong những toán tử quan trọng nhất trong cơ học lượng tử là Hamiltonian. Nó mô tả tập hợp mọi kết cục khả dĩ khi đo năng lượng toàn phần của một hệ lượng tử. Đối với một hạt đơn lẻ, về căn bản đây là tổng của các toán tử mô tả động năng của hạt đó (rút ra từ chuyển động và khối lượng), và thế năng (suy ra từ vị trí của nó trong một trường lực). Tuy nhiên, ta cũng có thể dùng Hamiltonian để mô tả các mức năng lượng nhúng trong một hệ, ví dụ như các mức năng lượng electron quay xung quanh một hạt nhân nguyên tử.
Mang tên nhà vật lí Ireland thế kỉ mười chín, William Hamilton, toán tử này có thể khác nhau tùy thuộc vào số lượng hạt trong hệ được đo. Nó giữ vai trò chính trong phương trình sóng Schrödinger phụ thuộc thời gian, trong đó nó sai khiến sự diễn tiến của hàm sóng theo thời gian. Các trị riêng phát sinh từ các nghiệm khả dĩ của phương trình tương ứng với các mức năng lượng gắn liền với những nghiệm đó.

Hình thức tích phân đường
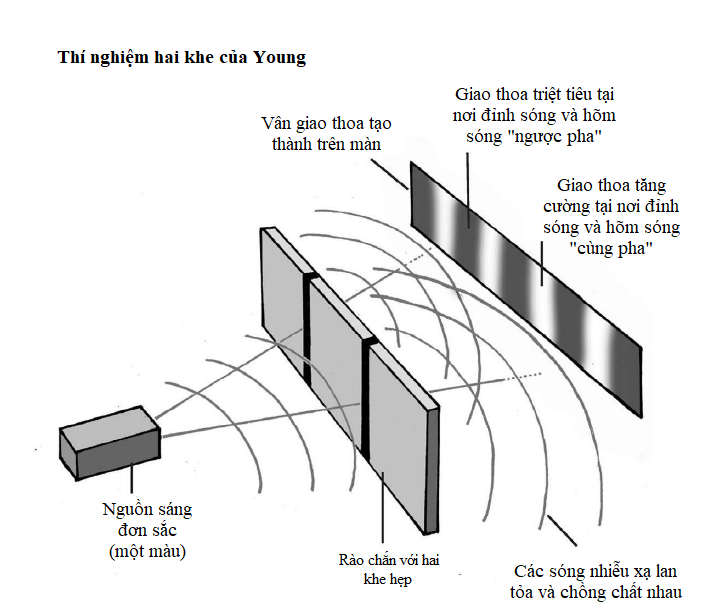
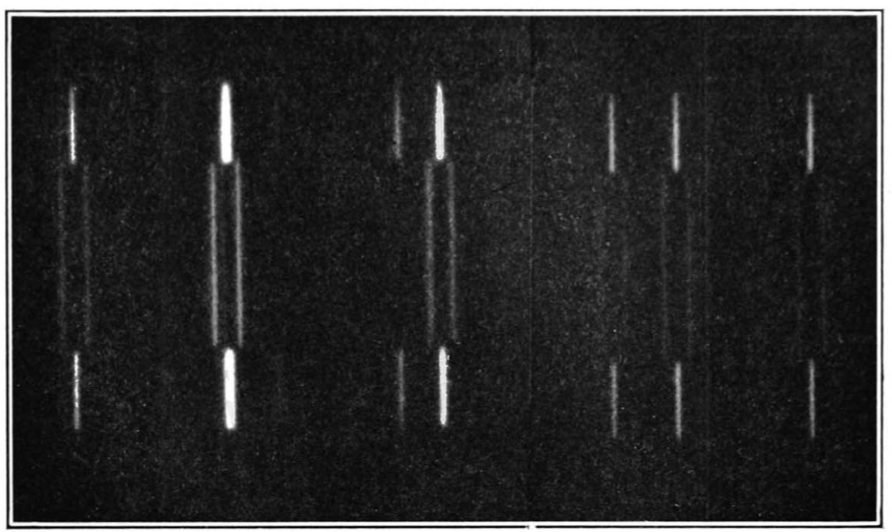
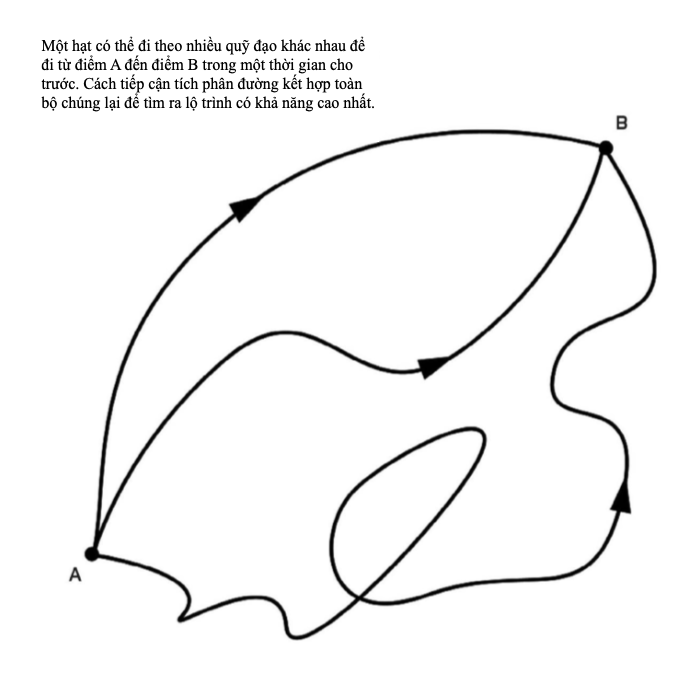
Như ta đã thấy, bí mật ẩn sau sự nhiễu xạ electron trong thí nghiệm hai khe là khả năng của một hạt biểu hiện hành trạng dạng sóng: một sóng có thể đi qua cả hai khe, trong khi theo vật lí cổ điển quỹ đạo của một hạt chỉ có thể đi qua một khe. Vì thế, hàm sóng của hạt đó là một phân bố xác suất, mô tả mọi quỹ đạo khả dĩ mà hạt có thể đi theo.
Tuy nhiên, việc biết được một hạt dạng sóng sẽ đi theo đường nào từ A đến B là chuyện bất định, vậy làm sao ta có thể xác định được quỹ đạo nào có khả năng cao nhất? Gần như có vô hạn hành trình khả dĩ, bao gồm cả những hành trình đi xuyên qua Vũ trụ rồi đi về. Chính Richard Feynman, một trong những trí tuệ lỗi lạc nhất của thế kỉ hai mươi, đã đi tới một kĩ thuật tính ra được đường đi có khả năng cao nhất của một hạt, dựa trên những ý tưởng ban đầu do Paul Dirac phát triển. ‘Hình thức tích phân đường’ của Feynman lấy tổng xác suất từ hàm sóng ứng với mỗi đường đi khả dĩ và kết hợp hoặc tích phân chúng về mặt toán học để tìm ra đường đi có khả năng cao nhất.
Vật lí Lượng tử Tốc hành | Gemma Lavender
Bản dịch của Thuvienvatly.com