79. Phải chăng phương trình bậc năm là không thể giải được bằng cách đưa nó về phương trình bậc bốn?
Chúng ta đã thấy rằng lời giải của một phương trình phụ thuộc vào lời giải của một phương trình bậc thấp hơn. Sử dụng nguyên lí này, một nhà toán học người Pháp, Lagrange, đã cố giải phương trình bậc năm nhưng nó lại dẫn ông tới một phương trình bậc sáu. Đây là một dấu hiệu gián tiếp rằng một phương trình bậc năm tổng quát không thể giải được bằng những phương pháp như thế. Lagrange đã bỏ qua gợi ý đó.
80. Abel đã chứng minh cái gì?
Abel, một nhà toán học người Na Uy, vào năm 1824 đã chứng minh kết quả nổi bật rằng phương trình đại số tổng quát có bậc cao hơn bốn là không thể giải được bằng cách khai căn.
81. Nhưng một số phương trình có bậc cao hơn bốn như x6 – 1 = 0 hoàn toàn có thể giải được bằng cách khai căn!
Các phương trình như x6 – 1 = 0, x8 – 2 = 0, xn – a = 0 hoàn toàn có thể giải được bằng cách khai căn mặc dù mỗi phương trình này có bậc cao hơn bốn. Không chỉ những phương trình này, mà còn nhiều phương trình khác có bậc tùy ý, chúng có thể được giải bằng phương pháp khai căn, cho nên vấn đề lúc này là xác định những điều kiện chính xác cho tính giải được của một phương trình theo căn thức.
82. Ai đã xác định được những điều kiện chính xác này?
Một nhà toán học người Pháp tên là Galois, ông qua đời trong một trận thách đấu phi lí lúc ở tuổi 21, đã đào sâu vấn đề và đã chứng minh vào năm 1831 rằng một phương trình đại số là có thể giải được theo căn thức nếu và chỉ nếu nhóm Galois của nó là có thể giải được. Phần chứng minh đó quá khó để trình bày ở đây.
83. Khi nào thì những phương pháp gần đúng được sử dụng?
Mặc dù một phương trình tổng quát có bậc cao hơn bốn là không thể giải được theo căn thức, nhưng nghiệm của một phương trình bất kì với các hệ số dạng số có thể được tìm ra đến độ chuẩn xác bất kì bởi cái gọi là những phương pháp gần đúng.
Có sẵn nhiều phương pháp và các phương pháp khác nhau thích hợp cho những phương trình khác nhau.
84. Những phương pháp này có thích hợp cho phương trình bậc ba và phương trình bậc bốn không?
Những phương pháp như thế thích hợp hơn cho việc giải các phương trình bậc ba và phương trình bậc bốn có các hệ số dạng số.
85. Một phương trình bậc ba được giải theo phương pháp đó như thế nào?
Phương pháp thông qua ở đây là thích hợp nếu phương trình đã cho có thể suy giản về dạng
x = a + Φ (x),
trong đó a là một con số nào đó, và Φf(x) là một đại lượng nhỏ phụ thuộc vào x.
Một nghiệm gần đúng được cho bởi x = a.
Đưa x = a vào vế phải của phương trình đã cho, ta thu được một gần đúng thứ hai,
x = a + Φ (a), trong đó Φ (a) là thay thế cho x trong Φ (x).
Kí hiệu giá trị này là a1, ta có một gần đúng thứ ba
x = a + Φ (a1)
và cứ thế, cho đến khi nghiệm đạt tới mức độ chuẩn xác theo yêu cầu.
86. Phương trình sau đây được giải như thế nào: x3 + 3x2 + 2 = 0?
Chia cho x2, phương trình đã cho có thể viết lại là
x = - 3 - 2/x2, có dạng x = a + Φ (x)
Một gần đúng thứ nhất là x = – 3.
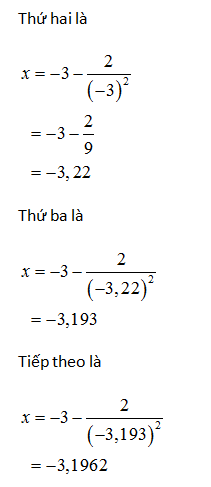
Phương trình này chỉ có một nghiệm thực. Hai nghiệm kia là ảo.
87. Các nghiệm của một phương trình được định vị như thế nào?
Khi một phương trình có nhiều hơn một nghiệm thực, để xác định tất cả các nghiệm, cần định vị chúng một cách gần đúng trước khi giá trị của chúng có thể được xác định đến độ chuẩn xác cần thiết.
Xét phương trình
8x3 – 100x2 + 342x – 315 = 0
Cho x nhận các giá trị 0, 1, 2, 3, 4, 5,… và duyệt qua giá trị của biểu thức ở vế trái. Ta hãy gọi nó là P, thì
P = 8x3 – 100x2 + 342x – 315
Khi x = 0, P = – 315
x = 1, P = – 65
x = 2, P = 33
x = 3, P = 27
x = 4, P = – 35
x = 5, P = – 105
x = 6, P = – 135
x = 7, P = – 77
x = 8, P = 120
Từ trên ta thấy khi x tăng từ 1 lên 2, P tăng từ – 65 lên 33. Bắt đầu từ một giá trị âm – 65, trước tiên P phải thu được một giá trị bằng không, và chỉ khi đó nó mới có thể tăng đến một giá trị dương 33. Do đó, P sẽ nhận một giá trị bằng không với một giá trị nào đó của x giữa 1 và 2.
Tương tự, khi x tăng từ 3 lên 4, giá trị của P giảm từ 27 xuống – 35. Do đó, một lần nữa P sẽ nhận một giá trị bằng không với một giá trị nào đó của x giữa 3 và 4.
Tiếp theo, khi x tăng từ 4 lên 7, P vẫn giữ nguyên dấu và không nhận một giá trị bằng không nào ở giữa khoảng đó.
Cuối cùng, khi x tăng từ 7 lên 8, giá trị của P tăng từ – 77 lên 120. Do đó, một lần nữa P sẽ nhận một giá trị bằng không với một giá trị nào đó của x giữa 7 và 8.
Vì một giá trị bằng không của P ứng với một nghiệm của phương trình, nên phương trình đã cho chỉ có các nghiệm giữa 1 và 2, giữa 3 và 4, và giữa 7 và 8.
Trong trường hợp đã cho, P nhận giá trị bằng không với x = 1,5; 3,5 và 7,5; đó là nghiệm của phương trình đã cho.
Toán học – Những điều kì thú và những mốc son lịch sử
A.L. Audichya
Trần Nghiêm dịch
Phần tiếp theo >>